randomGaussian() experiments

I recently started to play around with Processing and P5.js and while I’m not an expert yet I find I enjoy it very much.

I came across a Points Distribution dilemma post on r/processing subreddit where addictedtobiscuits is trying to recreate following image with processing.

Source: https://imgur.com/a/RXJxFtO

I thought that it would be an interesting challenge. I quickly put together a small sketch to recreate this effect and wanted to document my thought process. I’m very certain that this can be done in many different ways, but here is my approach and solution. But before we get into explanations I wanted to share my end result, which is fairly close to the image above.

I wrote my sketch in JavaScript using P5.js, but it can easily be converted into Java for Processing. There is a great primer on how Gaussian distribution works by Daniel Shiffman. If you haven’t seen his Coding Train videos I highly recommend it.

---

Here is my thought process and approach. For the sake of easier calculations I’m going to use 1000x1000px canvas.

Step 1: Let’s start with placing an imaginary rectangle on our canvas and adding random pixels to it.

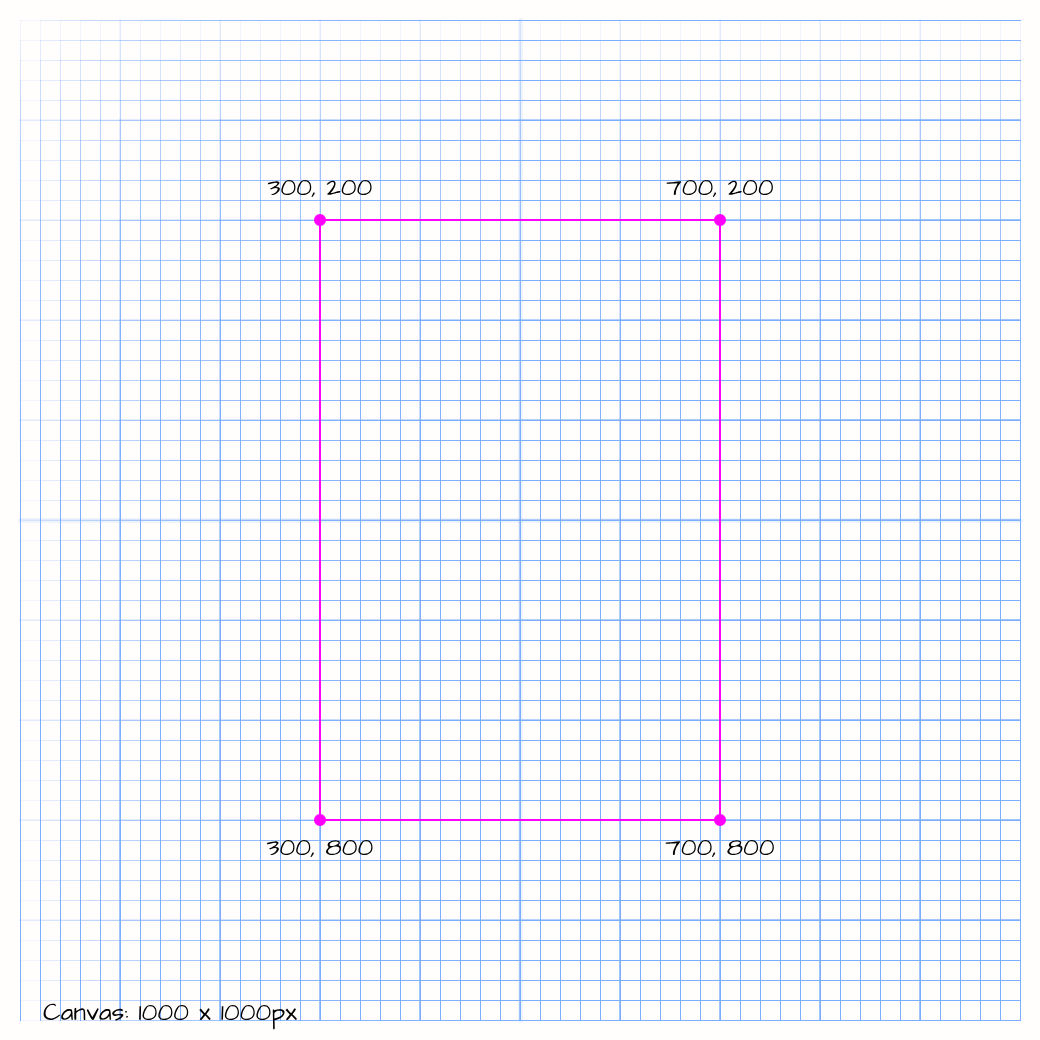
From the drawing above we can see that we our randomly placed points need to be placed between 300px and 700px on X axis and 200px and 800px on Y axis. We can translate that into code that looks something like this:

function setup() {
  createCanvas(1000, 1000)
  background(10)
}
function draw() {
  stroke(245)
  var xloc = random(300, 700)
  var yloc = random(200, 800)
  point(xloc, yloc)
}

and after running this for some time we should see something similar to the image below:

Step 1 is done. We have randomly located points constrained in a rectangle.

Step 2: That was easy. Now let’s try to figure out how we can do that with a trapezoid.

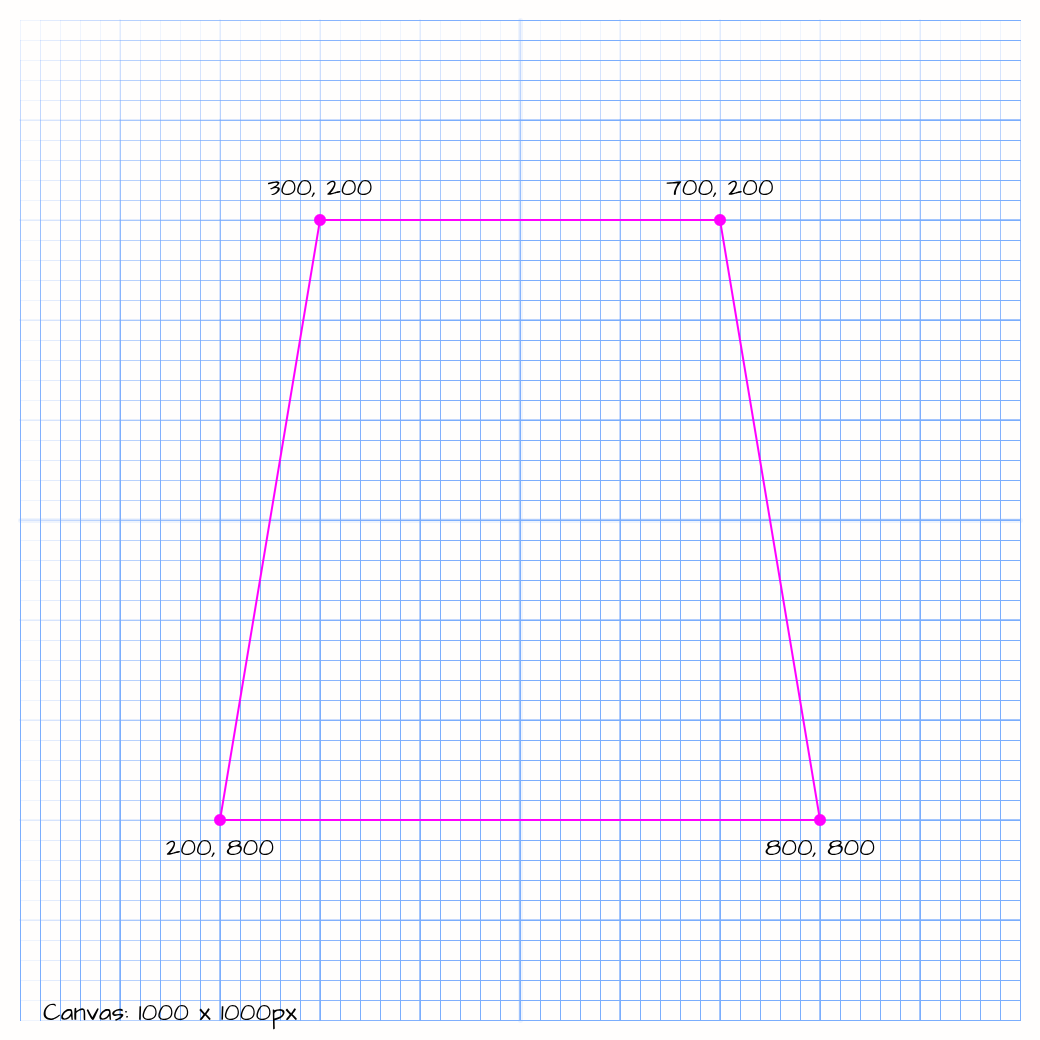
We will break this into 2 problems.

First one is a little easier. For Y axis our points need to be placed exactly the same as before, between 200px and 800px.

Second one for X axis may look a little tricky, but we have all the numbers to figure out where our random points should belong. Let’s look at the top, it seems the same, they should be between 300px and 700px. On the bottom of the trapezoid they should fall between 200px and 800px.

How do we calculate where points should fall anywhere between the top and the bottom? The answer is that we will use value of the yloc variable to help us with that. We know that it goes from 200px to 800px which means the height of the trapezoid is 600px. The bottom width of the trapezoid is 600px as well, which means when compared to the top it extends 100px to the left and 100px to the right on the bottom.

As yloc value increases (going from the top towards the bottom) we need to adjust xloc to be shifted up to 100px to the left and up to 100px to the right. In other words when yloc is 800px we need to make range of xloc to fall between 200px (300px — 100px = 200px) and 800px (700px + 100px = 800px).

Now we just need to figure out what that 100px in relation to the height of the trapezoid. (100 / 600) * 100 = 16.666666667% So at any given value of yloc our shift should be around 16.6% of yloc value. Because we are dealing with yloc (which falls into trapezoid boundaries), but starts with value of 200px we can say that our shift for X axis should be calculated as (yloc — 200) * 0.166.

Based on all of those things we can come up with a code to fill out our trapezoid with random points and not have any of them go out of trapezoids boundary. Keep in mind that we had to move up yloc assignment, because we need to have it declared and randomly picked in order to calculate xloc.

function setup() {
  createCanvas(1000, 1000)
  background(10)
}
function draw() {
  stroke(245)
  var yloc = random(200, 800)
  var shift = (yloc - 200) * 0.166
  var xloc = random(300 - shift, 700 + shift)
  point(xloc, yloc)
}

Executing this code will give us something like this:

Step 2 is done. We have placed random points inside of trapezoid. (Trapezoid boundary lines are drawn for illustration only and aren’t part of the code above)

Step 3: Let’s get to randomGaussian() already.

This part is fairly easy. We need to define our standard deviation (sd) and mean (mean) numbers.

We need to switch yloc calculation from using random() to use randomGaussian() method and do some very minor adjustments.

Let’s see how we can do that. For standard deviation we can pick an arbitrary number and see how well it works. Let’s pick 180. Knowing that Gaussian distribution produces both positive and negative numbers we will change all of them to be positive by using abs() function and then we will add mean of 200 to shift everything down by 200px (remember that’s where our top side of the trapezoid is). And then we constrain coordinates to fall between 200px and 800px to prevent an occasional point that drops below the trapezoid boundary. In code it will look like this:

var sd = 180
var mean = 200
var yloc = randomGaussian()
yloc = abs(yloc * sd) + mean
yloc = constrain(yloc, 200, 800)

I think we got all pieces of the puzzle and we are ready to put it together. With that our entire sketch would look like this:

var sd = 180
var mean = 200
function setup() {
  createCanvas(1000, 1000)
  background(10)
}
function draw() {
  stroke(245)
  var yloc = randomGaussian()
  yloc = abs(yloc * sd) + mean
  yloc = constrain(yloc, 200, 800)
  var shift = (yloc - 200) * 0.166
  var xloc = random(300 - shift, 700 + shift)

  point(xloc, yloc)
}

Voila! Here is our final result after running this sketch for some time:

Demo:

You can find code for this sketch and play with it on https://editor.p5js.org/morozgrafix/sketches/Hkkiu45pm

A slightly fancier version that produced header image for this post is available on https://www.openprocessing.org/sketch/627094

I have hardcoded most of the values for simplicity of this example, but this code can be adjusted to use values relative to dynamic width and height dimensions of the canvas.

Thanks and have a wonderful day!